Introduction to Geometry

Points, Vectors, Matrices 그리고 Normals는 CG에서 문학에서의 알파벳과 같은 것이다; 그래서 대부분의 CG책들은 선형대수학과 기하학에서 시작하는 것이 대다수이다. 그러나 그래픽스 프로그래밍을 배우고자 하는 많은 이들에게 이미지 하나 띄우는데 수많은 수학 이론을 들이미는 것은 꽤나 화가 치밀 것이다. 당신이 수학이 불편하거나matrix가 뭔지 모른다고 CG 프로그래밍은 내것이 아니라고 생각한다면, 아직 포기하지마라.

우리는 선형대수학에 대한 사전지식이 필요없는 몇몇 강의들로 “Foundation of 3D Rendering”을 시작했다. 이는 CG 프로그래밍을 가르치는 통상적인 방법은 아니지만, 뭔가 실용적이고 재미난 것으로 시작하는 것이 좀더 입문하는데 흥미로울 것이라 믿는다: 예를들어, 초반에 나오는Ray-tracer는 수학과 프로그래밍에 대한 지식을 아주 조금만 필요로한다.Renderer를 작성하는 것은, 당신이 수학과 같은 것들이 특정한 결과를 도출하는데 어떻게 사용되는지 점진적으로 관찰할 수 있으므로 더 흥미롭고 보람찬 일일 것이다. 다시 말하지만,Points,Vectors그리고Matrices는 CG 이미지들을 만드는 과정에서 필수적이다; 매 강의마다 그것들을 꽤나 광범위하게 사용하게 될 것이다.

이 강의에서, 당신은 이것들(points,vectors,matrices)이 무얼 만드는지, 어떻게 동작하는지 그리고 이들을 다루는 수많은 테크닉들에 대해서 배우게 될 것이다. 또한 이 강의에서는 지난 수년간 CG 연구원들이 사용해온, 기존의 선형대수학의 것과는 다른 convention에 대해서 설명할 것이다. 책에서는 이러한 convention들에 대해서 잘 언급하지 않기에 의식해 놓는 것이 좋다. 다른 개발자들의 코드나 테크닉을 읽고 사용하기 전에, 그들이 사용하는 convention을 먼저 확인하는 것이 좋다.

What is Linear Algebra? Introduction to Vectors

그래서 선형대수학이 정확히 무엇이고 이 강의에서 우리는 무얼 공부하게 되는가? 이전에 언급했듯, 선형대수학은vector에 대해 연구하는 수학의 한 분야이다. 그러면 당신은 이렇게 물을지도 모른다, “CG세계에서의Vector는 무엇이고 어떻게 유용하게 사용되는데?”. 너무 자세하게는 말하지 않겠지만,vector는 숫자들의 배열로 표현된다. 어떤 길이도 가질 수 있는 이 수들의 배열은 수학에서 때때로tuple이라고 불리기도 한다.Vector의 길이에 대해서 구체적으로 하자면,n-tuple이라고 말하는 것을 택하기도 한다(n은vector에서 원소의 개수). 아래는 6개의 원소를 가지는vector의 표현식의 예이다. \[V = (a, b, c, d, e, f)\]

이 때, a, b, c, d, e, f는 실수이다. 이 숫자들을 함께 묶는 아이디어의 뒤에는 어떤 문제의 맥락에서 집합적인 의미를 갖는 값 또는 개념을 의미한다.(The idea behind grouping these numbers together is that collectively they represent another value or concept that is meaningful in the context of the problem. - 애매..). 예를들어 CG에서, vectors는 공간에서의 위치 또는 방향을 나타내는데 사용될 수 있다. 또한 일련의 연산들을 통해 이러한vectors를 강력하고 촘촘한 방법으로 변환시킬 수 있다.vector의 내용을 변환하는 과정은 선형 변환(Linear Transformation)이라고 불리는 것에 의해 이뤄진다. 나중에 이런 변환들을 더 많이 설명하게 될 것이다; 지금은 이러한 변환이 왜 중요한지 인식하는 것만이 중요하다.

Points and Vectors

point와vector라는 용어는 많은 과학 분야에서 다양한 문맥에 사용되곤 했다. 이 단락에서, 두 용어 모두 이 튜토리얼과 CG와 관계지어 설명한다.

여기서point와vector는 3차원 공간에서 각각 위치와 방향을 의미한다.vectors는 다양한 방향을 가리키는 화살표로 생각해도 괜찮다. 3D 공간에서point와vector는 물론 앞에서 언급했듯tuple형태로 비슷하게 표현된다. \[V = (x, y, z)\]

이때 x, y, z는 실수이다.

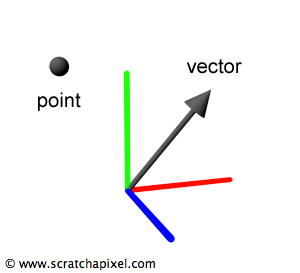
수학자와 물리학자와 이야기할 때, 그들의vector또는point cloud(점구름)은 좀 더 일반적인 것임을 기억하라; 그들은 우리가 그것들(points,vectors)을 사용하는 방법에 제한받지 않는다. 그들에게vector는 임의의 또는 무한한 크기를 가진다.

Homogeneous points(동차좌표)에 대해 짧게 언급하며 챕터를 끝내도록 하겠다. 때때로, 수학적 편의를 위해 4번째 원소를 추가하는 것이 필요하다.Homogeneous coordinates(동차좌표계)에서point의 예는 아래와 같다. \[P\_H = (x, y, z, w)\]

동차좌표는 점들을 행렬과 곱할 때 사용된다. 지금 이 시점에서선 너무 고민하지 않아도 된다. 문헌에서 종종 나오며 독자들에게 혼란을 줄 가능성이 있어 미리 언급한 것 뿐이다. 동차좌표와 동차좌표계에 대해서는 나중에 자세하게 설명할 것이다.

A Quick Introduction to Transformations

선형변환이 점과 벡터에 대해 주는 영향에 대해 궁금해 할지도 모르겠다. CG에서 가장 많이 수행하는 연산 중 하나는 간단하게 공간에서 이리저리 옮기는 것이다. 이러한 변환은 더 구체적으로translation이라고 부르며,rendering process에서 핵심적인 역할을 한다.

translation연산은 원점에 대한 선형변환일 뿐이다.vector에 적용하는 것은 아무런 의미가 없다. 이는vector가 어디서 시작하던 중요하지 않기 때문이다; 위치와 상관없이 길이가 같고 같은 방향을 가리키는 모든 화살표는 동일하다(equivalent). 대신,vector에많이 사용하는 다른 선형 변환으로rotation이 있다. 더 많은 연산자들이 사용될 수 있다, 하지만 지금은 점의translation과 벡터의rotation만 고려하도록 하자. \[P \\rightarrow Translate \\rightarrow P\_T\\ V \\rightarrow Rotate \\rightarrow V\_T\]

첨자로 표현된 T는 “변환됨(Transformed)”을 의미한다.

눈치 챘겠지만, 지금으로서는 길이가 무엇이고 크기가 무엇이며 벡터의 뜻이 뭔지 논의하는 것에는 실패했다. 실제로 벡터위 길이는 CG에서 대단히 중요하다. 벡터의 길이가 정확히 1일 때, 우리는 그 벡터를 정규화(normalized) 됐다고 한다. 정규화 하는 행동은 벡터의 방향은 그대로 두면서 길이만 1로 변화시키는 것이다. 대부분의 경우에 우리는 우리의 벡터가 정규화 되기를 원한다. 하지만, 가끔은 벡터의 길이가 의미있어서 정규화하지 않는 것을 선호하기도 한다.

예를들어 점A에서 점B로 선을 긋는 것을 상상해보자. 생성된 선분은 점A에 대해 상대적인 위치에 있는 점B를 나타내는vector이다. 즉, 그것은 점A의 위치에 있을 때, 점B를 향해 바라봄을 의미한다. 이 경우에vector의 길이는 점A와 점B 사이의 거리를 의미한다. 이런 거리는 가끔 특정 알고리즘에서 필요하다.

vectors의 정규화는 종종 프로그램 버그의 원인이기도 하며, 매번vector를 선언할 때마다 이vector가 정규화 되어야 하는지 아닌지를 스스로 항상 생각해보는 것이 좋다.

Normals

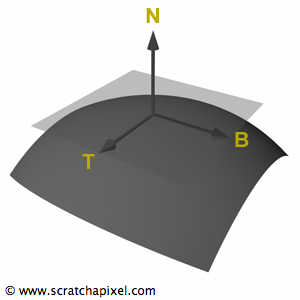
normal(법선)이란 CG에서 어느 한 표면 위에 있는 특정한 점에서 기하물체를 나타내는 기술적인 용어이다(A normal is the technical term used in Computer Graphics (and Geometry) to describe the orientation of a surface of a geometric object at a point on that surface.). 기술적으로, 점P에서 표면의surface normal은 점P에서 표면에 접하는 평면에 대해 수직인vector로 볼 수 있다.Normals는 물체의 밝기를 계산하는shading연산에서 중요한 역할을 한다.

Normal vector는 다른vectors과는 다른 방식으로 변환된다. 이것이normal을 다른vector들과 구분짓는 시간을 가진 이유이다. 이는 “Transforming Normals” 챕터에서 더 알아볼 수 있을 것이다. 지금은 그것들이 무엇인지 이해하는 것만 중요하다.

Summary

이 챕터에서, 수학적으로vector는 어떤 차원도 될 수 있음을 기억해야 한다. 그러나 CG에서vector는 3D 공간에서의 방향을 의미한다. 게다가,points는 3D 공간에서 위치를 의미한다.Homogeneous Points(동차좌표)는 4개의 숫자로 표현되며 이것은 특정한 경우로 나중에 배우기로 하겠다.

points와vectors는linear transformations(선형변환)으로 변환될 수 있다.

Linear Transformation이라는 용어는 나중에 종종 사용될 것이다. 만약 변환 이후에도 선들이 보존된다면 우리는 이를 두고linear transformation이라고 한다.

이러한 변환들의 전형적인 예로points의translation,vectors의rotation을 들 수 있다.vectors의 길이는 두 점사이의 거리를 의미하며 종종 특정 알고리즘에서 필요하다. 이러한 이유로 개발자는vector를 정규화 할지 말지 고민해볼 필요가 있다.

---

Original Lesson :

Geometry

이 번역글은 Scratchapixel에서 다국어 서비스를 시작하는 순간부터 비공개로 전환될 수 있습니다.

또한, 영어를 공부하고자하는 목적에서의 번역이기도 하므로 번역에 대한 지적은 환영입니다.